
...
http://www.reussirsavie.org/article-le-trefle-59186556.html
Le trèfle
Beaucoup de personnes n'avancent pas dans la vie car, lorsqu'une opportunité frappe à leur porte, ils sont derrière leur maison en train de chercher un trèfle à quatre feuilles.
Walter Chrysler
http://etab.ac-poitiers.fr/coll-marchioux/spip.php?article168
par F. Garoux
Atelier Tracé de courbes et Machines Mathématiques
Dans le cadre de la semaine des mathématiques du 12 au 17 mars 2012, dessin de LA BELLE HÉLÈNE, LE TRÈFLE À 4 FEUILLES,...pendant l’atelier "TRACÉ DE COURBES ET MACHINES MATHÉMATIQUES", animé par M. Garoux. L’atelier s'este déroulé le Mardi 13/3 de 12h30 à 13h30.
Site du collège du Marchioux
http://www.mathcurve.com/courbes2d/ornementales/ornementales.shtml
Trèfle de Brocard (1894, Loria p. 345)
Pour 3 feuilles :
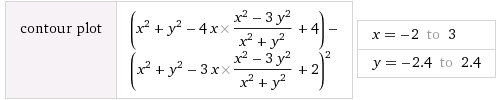
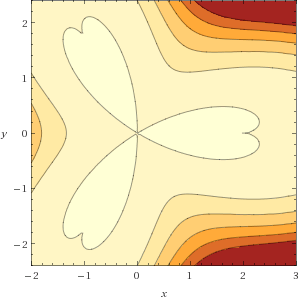
L'image représentée est un
graphique tracé à l'aide
du moteur de recherche
"Wolfram
Alpha"
à partir de l'expression ci-dessus
transcrite de la manière suivante :
implicitplot((x^2+y^2-4*x*(x^2-3*y^2)/(x^2+y^2)+4)-(x^2+y^2-3*x*(x^2-3*y^2)/(x^2+y^2)+2)^2,x=-2..3,y=-2.4..2.4);
les liens hypertextes associés : (votre navigateur est à jour et si possible google chrome, puis firefox )
http://www.mathcurve.com/courbes2d/ornementales/ornementales.shtml
Trèfle de Brocard (1894, Loria p. 345)
Pour 4 feuilles :
:
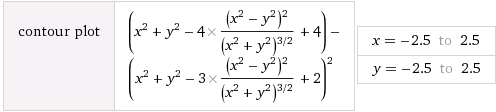
L'image représentée est un graphique
tracé à l'aide
du moteur de recherche "Wolfram
Alpha"
à partir de l'expression ci-dessus
transcrite de la manière suivante :
implicitplot((x^2+y^2-4*(x^2-y^2)^2/(x^2+y^2)^(3/2)+4)-(x^2+y^2-3*(x^2-y^2)^2/(x^2+y^2)^(3/2)+2)^2,x=-2.5..2.5,y=-2.5..2.5);
es liens hypertextes associés : (votre navigateur est à jour et si possible google chrome, puis firefox )