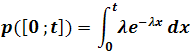|
1/ .
On s’intéresse
à la durée de vie, exprimée en semaines, d’un
composant électronique. On modélise cette situation par
une loi de probabilité p de durée de vie sans
vieillissement définie sur l’intervalle [0 ; +∞[ :
la probabilité que le composant ne
Une étude statistique, montrant qu’environ 50 % d’un lot important de ces composants sont encore en état de marche au bout de 200 semaines, permet de poser p([0 ; 200]) = 0,5. a/- Montrer que λ = ln 2 / 200. (ln2 vaut environ 0,693147181) b/Quelle est la probabilité qu’un de ces composants pris au hasard ait une durée de vie supérieure à 300 semaines ? On donnera la valeur exacte et une valeur approchée décimale (exp(-1) vaut environ 0,367879441 et exp(-1,1) = 0,332871084) c/ Quelle est la durée de vie moyenne d’un de ces composants ? d/ Quelle signification pouvez vous donner à l’égalité P(X>s+t / X>s) = P(X>t) pour tous réels positifs s et t ? e/ Pour tous réels positifs s et t, et pour toute variable aléatoire X suivant une loi analogue à celle étudiée plus haut montrer que P(X>s+t / X>s) = P(X>t)
2/ Une
machine automatique fabrique des tubes en série dont le
diamètre X est réparti selon la loi normale de moyenne a) Calculez la probabilité qu'une pièce prise au hasard dans la fabrication ait un diamètre compris entre 19,75 cm et 20,25 cm. b) Quel intervalle de centre 20 cm peut-on garantir avec une probabilité 0,95 ? c) On prélève un échantillon aléatoire de 20 tubes, et on accepte ceux dont le diamètre est compris entre19,71 cm et 20,29 cm.. Quelle est la probabilité qu’au moins 17 tubes soient acceptées ? d).
On appelle
e)
Calculer la Probabilité pour que l’écart de
3/ Est-ce que l’incompatibilité de deux événements A et B implique qu’ils sont indépendants ? Justifiez votre réponse.
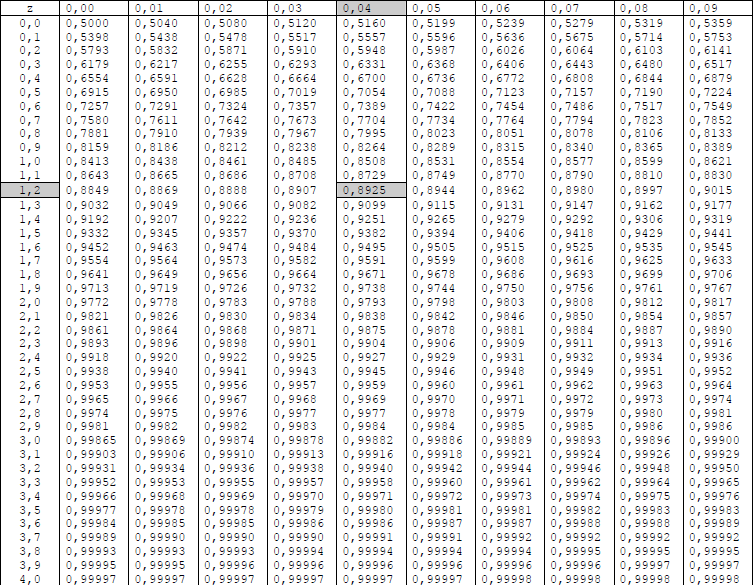
Annexe : Table de la fonction de répartition de N(0,1) |
20
la moyenne aléatoire des 20 tubes prélevées .
Quelle est la loi de
