1/

La consommation annuelle d’un ménage ayant un revenu R peut être considérée comme une variable aléatoire X ayant pour fonction de densité de probabilité f : où f(x)=kx⁷ si x appartient à [0 ; R ] et f(x)=0 sinon.

a/ Définir X(Ω).

b/Calculer en fonction de R l’espérance de X

c/ Calculer en fonction de R l’écart-type de X. (Donner le résultat de la variance en fraction de R et le coefficient de R dans l’écart-type en nombre décimal au dixième près ).

d/ Calculer la probabilité pour qu’un ménage consomme au moins les neuf dixièmes de son revenu.

Eléments de correction

2/

Une enquête est effectuée auprès de familles de 4 personnes afin de connaître leur achat de lait en 1 mois. Sur l'ensemble des personnes interrogées, la consommation de ce produit forme une population gaussienne avec une moyenne de 20L et un écart-type de 6 (Ce qui signifie que la variable aléatoire « consommation de lait en litre en 1 mois d’une famille » suit une loi normale d’espérance 20 et d’écart-type 6). En vue d'une conception d'une campagne de pub, on souhaite connaître la probabilité pour qu’une famille soit considérée comme « faible consommateur » (c'est-à-dire moins de 10 L/mois) et la probabilité pour qu’une famille soit considérée comme « grand consommateur » (c'est-à-dire plus de 30 L/mois).

Questions :

1. Calculer ces 2 probablités.

2. On sait que la probabilité pour qu’une famille consomme au-dessous d’un nombre de litres acheté dans le mois est de 75%. Quelle est cette quantité ?

3. Combien de litres au maximum consomme la moitié des familles consommatrices de lait?

Eléments de correction

3/

Soit Ω un univers et ces deux événements A et B tel que
A U B = Ω, Prob(A)= 0,5 et Prob(B) = 0,7. Ces valeurs numériques sont elles possibles ? Si oui quelle en est la conséquence ?, si non dites pourquoi. ?

Eléments de correction

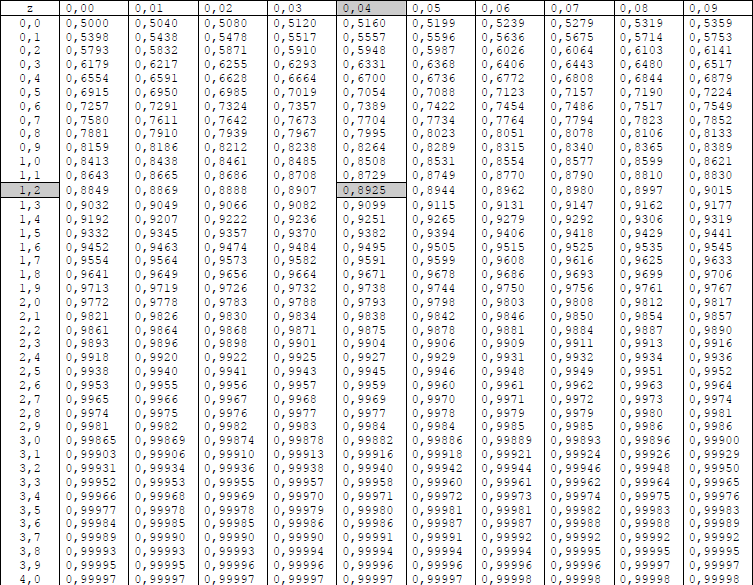
Annexe : Table de la fonction de répartition de N(0,1)