Attention : Les résultats non justifiés ne sont pas pris en compte ;
Rappel : A l’examen les calculatrices sont interdites

(cet énoncé en PDF)

Exercice 1

Décrire les axiomes qui permettent à un ensemble E muni de deux lois : l’une interne notée ⊕ et l’autre externe par rapport à R notée ⊗ soit un espace vectoriel sur R

( Correction )

Exercice 2

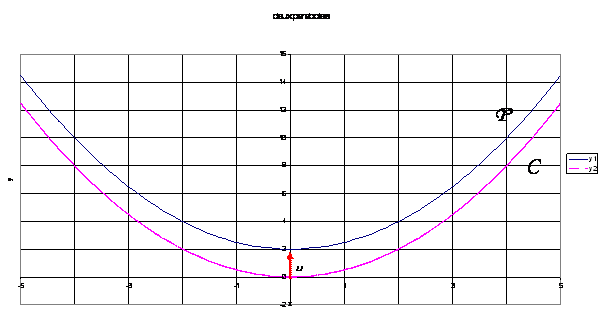
A partir des représentations graphiques (P) ou (C), suivantes , dites laquelle correspond à celle d’un sous-espace vectoriel et laquelle à celle d’une variété affine.

( Correction )

Exercice 3

On se place dans l'espace vectoriel R². On notera x = (x_l, x₂) les éléments

de R² ..

1./Enoncez ce qu’il faut démontrer pour que D = {x ∈ R².; x_l + x₂ = O} et K = { x ∈ R².; x_l - x₂ = O } soient des sous-espace vectoriels de R² et indiquez à quel ensemble appartient le O écrite dans x_l + x₂ = O dans l’expression de D.

2/ en donner une représentation graphique de D et K

3/ Donnez une variété affine A de direction D

4/ en donner une représentation graphique de A

5/ Dessinez dans le graphique deux éléments de A

6/ Enoncez ce qu’il faut démontrer pour que D et K soient deux sous espaces supplémentaires

7/ Démontrez que D ∩ K = {O_R2}

( Correction )

Exercice 4

M={(x,y,z)ÎR³, x=2, y=1, z=-3, }, est ce que M est une variété affine ?

( Correction )

Exercice 5a

l’ensemble A={(x,y) ∈R², y+2x²=0} est –il un sous espace vectoriel de R²?

( Correction )

Exercice 5b

Soit u₁ =(1,1,1) ; u₂=(1,1,-1) ; u₃=(1,-1,1), u₄=(2,2,-2) ; u₅=(3,1,-1) et E le sous-espace vectoriel de R³ engendré par la famille U={ u₁ , u₂ ,u₃, u₄, u₅ }

1/ Extraire de la famille U une base B de E. En déduire que E=R³

( Correction )